【金融知识】国债期货转换因子的推导与理解
背景
在国债期货到期日,现货市场往往存在多个符合交割标准的债券,国债期货在交割中设计了转换因子制度。在转换因子制度下,每只可交割债券都有其相应的转换因子,通过转换因子可计算该可交割债券的交割价格。
要理解国债期货转换因子这个概念,还需要对国债期货本身的特征有一定的了解。首先要了解国债期货中的标准券:国债期货是标准化合约,合约标的是一个名义标准券,也可以说是虚拟券,这个设计的最大功能,就是可以扩大可交割国债的范围,增强价格的抗操纵性,减小交割时的逼仓风险。但是事实上,国债期货采用实物交割,空头交割时理论上需要用名义标准券去履约。但现实中名义标准券并不存在,因而交易所规定可以使用现实中存在的、满足一定期限要求的一篮子国债均可进行交割。但是在金融市场中,金融产品在价格上必须满足一对一的映射才能保证定价体系的平衡,否则会出现无风险套利机会。转换因子(Conversion Factor, CF) 就是实现一对一映射的纽带。
在我国各类国债期货中,他们对应的标准券如下:
2年期国债期货合约标的:面值为200万元人民币、票面利率为3%的名义中短期国债;
5年期国债期货合约标的是:面值为100万元人民币、票面利率为3% 的名义中期国债;
10年期国债期货合约标的:面值为100万元人民币、票面利率为3%的名义长期国债。
公式介绍
现在给出中金所计算转换因子的公式:
其中,
r:10年期国债期货合约票面利率3%;
x:交割月到下一付息月的月份数;
n:剩余付息次数;
c:可交割国债的票面利率;
f:可交割国债每年的付息次数;
计算结果四舍五入至小数点后4位。
推导过程
首先思考如何从金融的逻辑上去理解这个公式,假设现在国债期货价格为1,那么如果想要用其他债券去平掉当前仓位,就需要看其他债券的价格与标准券想必是
设想一个场景,在国债市场上存在一份5年期国债期货合约,我们希望用三年期的5%利率国债进行交割。此时,为了保证二者收益相等,就需要采用某个权值,将一系列的交割债券转换为作为标的物的标准券,保证二者收益一致,从而达到交割效果。这个权值就是转换因子。转换因子的实质就是面值1元的可交割国债在其剩余期限内所有现金流按照国债期货合约的票面利率折现的现值。
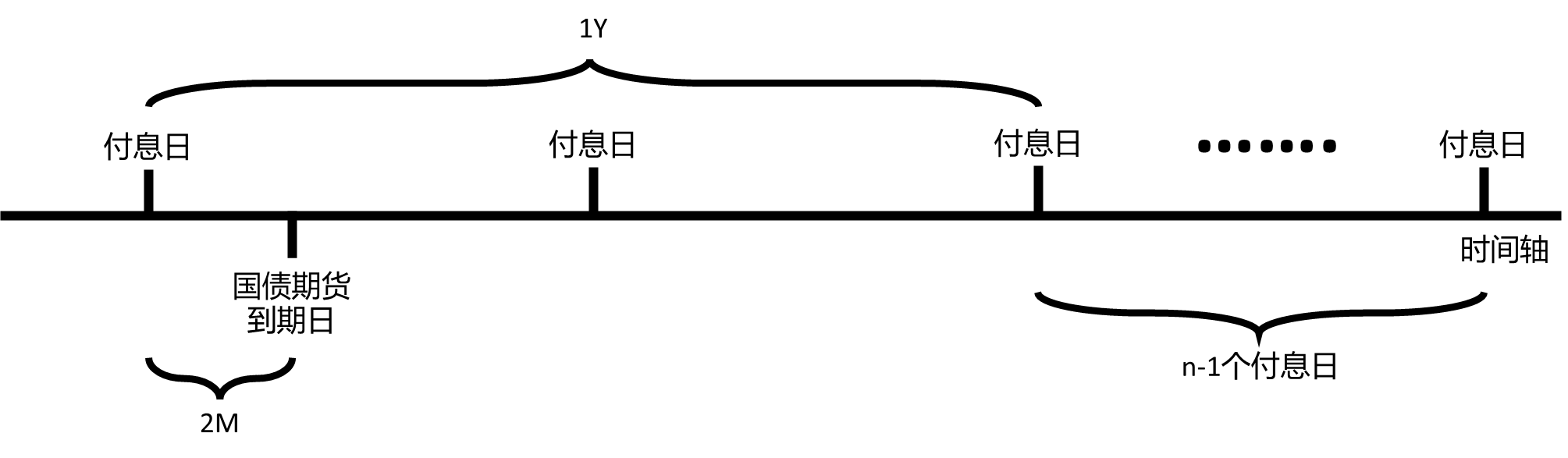
有了这个思路,我们就可以计算了:
首先,将债券未来现金流贴现至期货到期日后的第一个付息日,其中包括票息的折现与面值的折现。此时,债券还有n次票息未支付,每次支付的票息为,折现利率就是:
利用等比数列求和公式化简一下:
\begin{flalign} \nonumber P_1 = \sum_{i=0}^{n-1} \frac{\frac{c}{f}}{(1+\frac{r}{f})^{i}}+\frac{1}{(1+\frac{r}{f})^{n-1}} &= \frac{c}{f}\frac{1-(\frac{1}{1+\frac{r}{f}})^n}{1-\frac{1}{1+\frac{r}{f}}}+\frac{1}{(1+\frac{r}{f})^{n-1}} \\ &= \frac{c}{f}\frac{1+\frac{r}{f}-(\frac{1}{1+\frac{r}{f}})^{n-1}}{\frac{r}{f}}+\frac{1}{(1+\frac{r}{f})^{n-1}} \\ &= \frac{c}{r}+\frac{c}{f}-\frac{c}{r}\frac{1}{(1+\frac{r}{f})^{n-1}}+\frac{1}{(1+\frac{r}{f})^{n-1}} \\ &= \frac{c}{r}+\frac{c}{f}+(1-\frac{c}{r})*\frac{1}{(1+\frac{r}{f})^{n-1}} \nonumber \end{flalign}
如此一看,公式中间部分是不是就出来了!
将现金流进一步折现至期货到期日,此时还有x月就付息了,所以折现期为x月,对应的折现因子为:
所以,到期日债券全价为:
最后将债券当前的累计利息减掉
由此得到债券净价,也就是转换因子的最终公式:






